![]()
이번 칼럼에서는 사람의 사고 방식과 판단 방법에 대해 고민해볼 수 있게 해주는 두 가지 역설을 소개해보려고 합니다.
(1)상트페테르부르크 역설

상트페테르부르크의 모습
상트페테르부르크는 러시아의 도시 이름인데, 이 역설에 대해 다룬 천재 수학자 다니엘 베르누이의 논문 '위험 측정에 관한 새로운 이론의 해설'이 상트페테르부르크에서 출판되었기 때문에 이런 이름이 붙었을 뿐, 문제의 내용과는 무관합니다.

라틴어로 된 다니엘의 실제 논문 표지
참고로 이 역설을 처음 발견한 것은 다니엘의 사촌형 니콜라우스 베르누이라고 합니다. 다니엘만큼은 아니지만 이 사람도 천재입니다.
이 역설을 이해하려면 먼저 기댓값에 대해 알아야 합니다. 도박에서 수익의 기댓값은, 말 그대로 도박을 했을 때 평균적으로 얻으리라고 기대되는 금액입니다. 도박의 기댓값을 계산하는 방법은 다음과 같습니다.
돈을 따게 될 확률 × 그 때 받게 되는 금액
예를 들어 동전을 한번 던져서 앞면이 나오면 100만원을 받는 도박의 기댓값은 1/2 곱하기 100만원 = 50만원이 됩니다. 기댓값은 말 그대로 도박에서의 예상 수익이기 때문에, 50만원보다 적은 돈을 내고 이 도박에 참여할 수 있다면 이득을 보는 셈입니다. 49만원을 내라고 하면 모르겠지만, 5만원을 내고 이 도박을 해보라고 하면 거의 모든 사람이 응할 것 같습니다.
그런데 상트페테르부르크 역설에서는 다음과 같은 게임이 제시됩니다.
1.동전에서 앞면이 나오면 한번 더 던진다.
2.뒷면이 나오면 그만하고 돈을 받는다.
3.받는 금액은 동전을 한번 더 던지게 될 때마다 두배로 늘어난다.
동전을 던져서 첫번째에 뒷면이 나오면 1만원, 두 번째에 뒷면이 나오면 2만원, 세 번째에 뒷면이 나오면 4만원을 받는 것입니다.
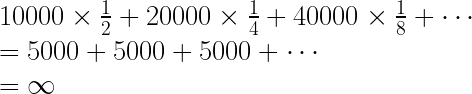
이 게임의 기댓값 계산
이 게임의 기댓값을 계산해보면 무한대입니다. 무한한 이득이 기대되기 때문에, 얼마를 내더라도 이 게임을 해야할 것처럼 보입니다. 하지만 실제로는 아무도 이 도박에 큰 돈을 쓰려고 하지 않습니다. 여러분은 100만원을 내고 이 게임을 하실 건가요?
수학적으로 기댓값이 무한대인 건 확실한데, 아무도 그렇게 생각하지는 않는다는 것이 이 역설의 핵심입니다.
이 역설은 한가지 정답이 있는 문제는 아닙니다. 하지만 여러 가지 해석과 설명이 나왔고 그 중에서 몇 가지만 소개해보겠습니다.
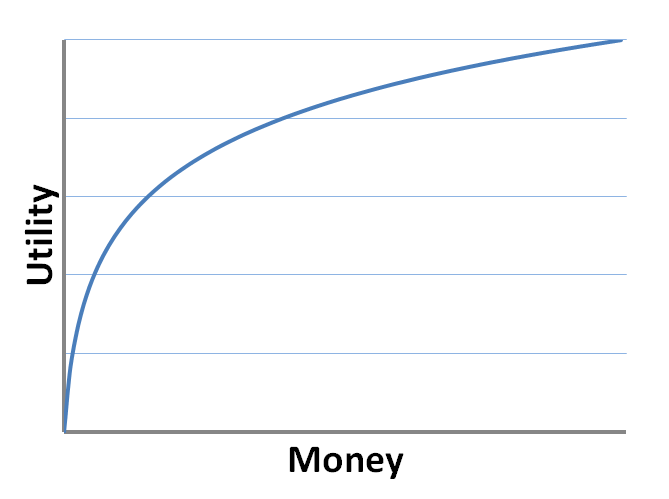
돈이 늘어나는 만큼 효용도 늘어나는 건 아니라는 걸 보여주는 그래프
가장 유명한 설명은 이 문제를 처음 다룬 다니엘 베르누이가 제시한 기대효용 가설입니다. 단순히 받는 금액이 아니라 얻게 되는 효용이 게임의 가치를 정한다는 주장입니다.
이 주장에 따르면, 받는 돈은 정확히 두 배씩 늘어나지만, 돈을 두배로 받는다고 기쁨과 만족감 등의 효용이 정말 2배로 늘어나는 건 아니기 때문에, 게임의 가치는 무한대가 아닌 특정한 값으로 수렴합니다. 다니엘은 구체적으로 효용이 위의 그래프처럼 로그함수 꼴이라고 주장했습니다.
금액이 아니라 효용을 따져야 한다는 것은 굉장히 뛰어난 아이디어이고, 경제학에도 큰 영향을 미쳤습니다. 다만 게임 자체가 이론적인 상황이기 때문에, 게임에서 사용되는 함수를 조금 바꾸면 효용도 무한대로 만들 수 있다는 비판이 제기됩니다. (카를 멩거의 말대로, n번째에 받는 돈이 2^(2^n)이면 효용의 기댓값도 무한대가 됩니다.)
일반인들은 고려하지 않는 낮은 확률의 기적
다른 설명은 사람은 아주 낮은 확률은 무시한다는 것입니다. 이건 니콜라우스 베르누이의 설명인데, 이것도 설득력이 있습니다. 이 게임에 대해 고려할 때 1/1073741824의 확률로 5조 3700억원을 벌 수 있다는 생각을 하는 사람은 없을 것 같습니다.
그 외에 현실적으로 무한한 돈도 없고, 동전을 계속 던질 무한한 시간도 없다는 주장이 있습니다. 또 경제학자 폴 새뮤얼슨은 도박의 수익의 기댓값이 무한대라는 건 돈을 주는 쪽의 손실 기댓값이 무한대라는 소리이기 때문에 돈이 정말로 무한히 있어도 이런 도박은 불가능하다는 점을 지적하기도 했습니다.

기댓값이 판매가격보다 낮은 로또
상트페테르부르크 역설은 많은 후속 연구를 낳았고, 경제학에도 큰 영향을 미쳤지만 무엇보다도 수학적 기댓값은 사실 도박에서 그렇게 중요한 부분이 아니라는 걸 말해주는 것 같습니다. 오늘도 사람들은 로또의 기댓값이 판매가격보다 낮다는 걸 알면서도 로또를 사고 있습니다.
(2)엘스버그 역설

다니엘 엘스버그의 젊은시절 모습
먼저 이 역설을 유명하게 만든 다니엘 엘스버그에 대해 간단히 소개하겠습니다. 그는 미국에서 1931년에 태어나 아직도 살아있는데, 특이한 이력과 펜타곤 반전운동으로도 매우 유명합니다. 엘스버그는 하버드를 최우등 졸업한 뒤 해병대에 입대해 군복무를 하고 전역해 다시 하버드에서 경제학 박사 학위를 땄고, 그 뒤 전쟁과 국가 안보를 다루는 민간 싱크탱크인 랜드연구소에서 일했습니다.

펜타곤 페이퍼를 폭로한 뉴욕타임스 1면
그러던 중 그는 소위 '펜타곤 페이퍼' 작성에 참여하게 됩니다. 펜타곤 페이퍼는 미국의 베트남 전쟁에 관한 실상을 담은 국방부 기밀 보고서였는데, 엘스버그는 펜타곤 페이퍼를 작성하면서 베트남 전쟁에 회의감을 느끼고, 1971년 펜타곤 페이퍼를 복사해 뉴욕타임스에 전달, 그 내용을 폭로합니다. 그는 이 일로 기소되어 115년형을 선고받지만 결국 연방대법원에서 무죄 판결을 받고 풀려납니다.
엘스버그에 대한 설명은 이쯤하고, 이제 엘스버그 역설에 대해 본격적으로 이야기하겠습니다. 엘스버그 역설은 엘스버그가 최초로 발견한 것은 아니지만, 1961년 랜드연구소에서 일하던 엘스버그가 쓴 논문 때문에 유명해졌기 때문에 그런 이름이 붙었습니다.

안에 공이 든 주머니
해당 논문에서 엘스버그가 제시한 실험은 다음과 같습니다.
1)공이 주머니 안에 90개 들어있다.
2)그 중에서 30개는 빨강이고, 나머지는 검정과 노랑이 섞여있다.
3)검정과 노랑이 각각 몇개씩 있는지는 모른다.
실험 참가자들에게 이 사실을 알려준 뒤, 이렇게 제안한다.
A1)주머니에서 꺼낸 공이 빨강이면 100달러를 주겠다. 다른 색이면 돈을 받지 못한다.
A2)주머니에서 꺼낸 공이 검정이면 100달러를 주겠다. 다른 색이면 돈을 받지 못한다.
두 제안 중에서 하나를 고르도록 한다.
또한
B1)주머니에서 꺼낸 공이 검정이거나 노랑이면 100달러를 주겠다. 빨강이면 돈을 받지 못한다.
B2)주머니에서 꺼낸 공이 빨강이거나 노랑이면 100달러를 주겠다. 검정이면 돈을 받지 못한다.
이 중에서도 하나를 고르도록 한다.
실험 결과 거의 모든 실험 참가자들은 A1과 B1을 골랐습니다.
A1은 당첨될 확률이 1/3, B1은 당첨될 확률이 2/3으로 명확하기 때문입니다.
그런데 이 결과는 논리적으로 부당합니다. 왜냐하면 A1을 골랐다는 것은 주머니에 빨강이 검정보다 더 많다고 생각했기 때문이고, 그렇다면 B1과 B2 중에서는 B2를 고르는 것이 유리하기 때문입니다.
또 A1을 골라서 얻는 효용이 A2보다 크고, B1를 골라서 얻는 효용이 B2가 주는 효용보다 크다면 (A1-B1)이 주는 효용은 (A2-B2)가 주는 효용보다 커야합니다. 그렇지만 (A1-B1)과 (A2-B2)는 둘 다 100% 확률로 100달러를 받게되는, 효용이 동일한 행위입니다.
이렇게 보면 실험 참가자들이 멍청해 보이지만, 엘스버그의 실험에 참가한 사람들은 유명한 경제학자들이었습니다.
이 역설은 보통 '사람은 불확실성을 싫어한다'는 식으로 해석됩니다.
이렇게 불확실성을 피하는 것 자체는 비합리적이지 않지만, 그 과정에서 비합리적인 행동을 할 수 있다는 사실에 주의할 필요가 있는 것 같습니다.
두 역설은 모두 수학적 논리와 사람의 직관이 얼마나 크게 차이나는지를 보여줍니다. 하지만 상트페테르부르크 역설에서는 직관이, 엘스버그 역설에서는 수학적 논리가 좀 더 옳은 것 같습니다. 사람이 늘 논리적인 판단을 하는 것은 아니지만, 한편으로는 그럴만한 이유가 있다는 것도 알 수 있었습니다. 상식과 수학이 상충될 때 한쪽을 배제하려는 태도보다는, 그 원인을 분석하고 살펴보는 것이 좋은 것 같습니다.





 추천
추천















