츄잉~ chuing~

함수 $fcolon Eto {mathbb R}$ ( ${displaystyle Esubseteq mathbb {R} ^{n}}$ 은 조르당 가측 집합)의, 분할 ${displaystyle {E_{i}}_{i=1}^{m}subseteq {mathcal {P}}(E)}$ 에 대한 리만 합(영어: Riemann sum)은 다음과 같다.

{displaystyle sum _{i=1}^{m}f(xi _{1}^{(i)},dots ,xi _{n}^{(i)})operatorname {m} (E_{i})qquad (xi _{1}^{(i)},dots ,xi _{n}^{(i)})in E_{i}}

또한, 다르부 상합(영어: upper Darboux sum)은 다음과 같다.

{displaystyle sum _{i=1}^{m}sup _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})}

또한, 다르부 하합(영어: lower Darboux sum)은 다음과 같다.

{displaystyle sum _{i=1}^{m}inf _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})}

함수 $fcolon Eto {mathbb R}$ ( ${displaystyle Esubseteq mathbb {R} ^{n}}$ 은 조르당 가측 집합)에 대하여, 만약 다음과 같은 극한이 존재하며, 분할 ${displaystyle {E_{i}}_{i=1}^{m}}$ 및 각 집합의 점 ${displaystyle (xi _{1}^{(i)},dots ,xi _{n}^{(i)})}$ 의 열의 선택과 무관하다면, $f$ 를 $E$ 위의 리만 적분 가능 함수(영어: Riemann integrable function)라고 하며, 이 극한을 $f$ 의 리만 $n$ 중적분(영어: n-ple Riemann integral)이라고 한다.

{displaystyle int _{E}f(x)dx=iint cdots int _{E}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=lim _{lambda ({E_{i}}_{i=1}^{m})to 0}sum _{i=1}^{m}f(xi _{1}^{(i)},dots ,xi _{n}^{(i)})operatorname {m} (E_{i})}

또한, 다르부 상적분(영어: upper Darboux integral)은 다음과 같으며, 이는 항상 존재한다.

{displaystyle {begin{aligned}{overline {int _{E}}}f(x)dx={overline {iint cdots int _{E}}}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}&=lim _{lambda ({E_{i}}_{i=1}^{m})to 0}sum _{i=1}^{m}sup _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})&=inf _{{mathcal {P}}(E)supseteq {E_{i}}_{i=1}^{m}in operatorname {dom} lambda }sum _{i=1}^{m}sup _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})end{aligned}}}

마찬가지로, 다르부 하적분(영어: lower Darboux integral)은 다음과 같으며, 이는 항상 존재한다.

{displaystyle {begin{aligned}{underline {int _{E}}}f(x)dx={underline {iint cdots int _{E}}}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}&=lim _{lambda ({E_{i}}_{i=1}^{m})to 0}sum _{i=1}^{m}inf _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})&=sup _{{mathcal {P}}(E)supseteq {E_{i}}_{i=1}^{m}in operatorname {dom} lambda }sum _{i=1}^{m}inf _{(x_{1},dots ,x_{n})in E_{i}}f(x_{1},dots ,x_{n})operatorname {m} (E_{i})end{aligned}}}

특히, 리만 이중 적분을

{displaystyle iint _{E}f(x,y)dxdy=iint _{E}f(x,y)dA=lim _{lambda ({E_{i}}_{i=1}^{m})to 0}sum _{i=1}^{m}f(xi _{i},eta _{i})operatorname {m} (E_{i})}

와 같이 표기하며, 리만 삼중 적분을

{displaystyle iiint _{E}f(x,y,z)dxdydz=iiint _{E}f(x,y,z)dV=lim _{lambda ({E_{i}}_{i=1}^{m})to 0}sum _{i=1}^{m}f(xi _{i},eta _{i},zeta _{i})operatorname {m} (E_{i})}

와 같이 표기한다.

이상 리만 중적분[편집]

유계 집합과 (정의역이 조르당 영집합이 아니라면) 유계 함수에 한정된 리만 중적분을 무계 집합과 무계 함수를 허용하는 이상 리만 중적분(영어: improper multiple Riemann integral)으로 확장할 수 있다. 일변수 함수에서와 달리, 이상 리만 중적분이 수렴할 필요충분조건은 절대 수렴한다는 것이다.

함수 $fcolon Eto {mathbb R}$ 및 그 정의역 ${displaystyle Esubseteq mathbb {R} ^{n}}$ 이 다음 조건들을 만족시킨다고 하자.

$E$ 는 무계 집합이다.
$f$ 는 유계 함수이다.
임의의 {displaystyle r>0} $r>0$ 에 대하여, {displaystyle Ecap {bar {B}}_{R}(0)} ${displaystyle Ecap {bar {B}}_{R}(0)}$ 는 조르당 가측 닫힌집합이다.
- 여기서 ${displaystyle {bar {B}}_{R}(0)={(x_{1},dots ,x_{n})colon x_{1}^{2}+cdots x_{n}^{2}leq R^{2}}}$ 은 닫힌 공이다.
- 특히, $E$ 가 무계 닫힌집합일 경우, ${displaystyle Ecap {bar {B}}_{R}(0)}$ 가 닫힌집합이라는 조건은 생략할 수 있다.
임의의 조르당 가측 닫힌집합 ${displaystyle Fsubseteq E}$ 에 대하여, $f$ 는 $F$ 에서 리만 적분 가능 함수이다.

이러한 $f$ 및 $E$ 에 대하여, 다음과 같은 극한이 존재하며, 조르당 가측 닫힌집합 ${displaystyle Fsubseteq E}$ 의 열의 선택과 무관하다면, 이를 $f$ 의 $E$ 위의 이상 리만 중적분이라고 한다.

{displaystyle iint cdots int _{E}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=lim _{sup{r>0colon Fsupseteq Ecap {bar {B}}_{R}(0)}to infty }iint cdots int _{F}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}}

비슷하게, ${displaystyle Esubseteq mathbb {R} ^{n}}$ 및 ${displaystyle (a_{1},dots ,a_{n})in E}$ 및 ${displaystyle fcolon Esetminus {(a_{1},dots ,a_{n})}to mathbb {R} }$ 가 다음 조건들을 만족시킨다고 하자.

$E$ 는 유계 집합이다.
$f$ 는 무계 함수이다.
임의의 {displaystyle r>0} $r>0$ 에 대하여, {displaystyle Esetminus B_{R}(a)} ${displaystyle Esetminus B_{R}(a)}$ 는 조르당 가측 닫힌집합이다.
- 여기서 ${displaystyle B_{R}(a)={(x_{1},dots ,x_{n})colon (x_{1}-a_{1})^{2}+cdots +(x_{n}-a_{n})^{2}leq r^{2}}}$ 는 열린 공이다.
- 특히, $E$ 가 조르당 가측 닫힌집합일 경우, 이 조건은 생략할 수 있다.
임의의 조르당 가측 닫힌집합 ${displaystyle Fsubseteq Esetminus {(a_{1},dots ,a_{n})}}$ 에 대하여, $f$ 는 $F$ 에서 리만 적분 가능 함수이다.

이러한 $f$ 및 $E$ 에 대하여, 다음과 같은 극한이 존재하며, 조르당 가측 닫힌집합 ${displaystyle Fsubseteq Esetminus {(a_{1},dots ,a_{n})}}$ 의 열의 선택과 무관하다면, 이를 $f$ 의 $E$ 위의 이상 리만 중적분이라고 한다.

{displaystyle iint cdots int _{E}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=lim _{inf{r>0colon Fsupseteq Esetminus B_{R}(a)}to 0^{+}}iint cdots int _{F}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}}

르베그 중적분[편집]

르베그 중적분(영어: multiple Lebesgue integral)은 유클리드 공간의 르베그 측도에 기반하여 정의된다.

성질[편집]

리만 적분 가능 함수는 유계 함수일 필요가 없다. 예를 들어, 정의역이 조르당 영집합인 함수는 항상 리만 적분 가능 함수이다. 그러나, 양의 조르당 측도의 집합들로 임의로 세밀하게 분할될 수 있는 정의역 위의 리만 적분 가능 함수는 항상 유계 함수이다. 특히, 조르당 가측 열린집합 또는 그 폐포 위의 리만 적분 가능 함수는 항상 유계 함수이다.^[2]

리만 중적분은 일변수 함수의 리만 적분과 같은 성질들을 갖췄다. 예를 들어, 리만 중적분은 선형성 · 적분 집합에 대한 가법성 · 비엄격 부등식의 보존 · 곱의 적분 가능성 보존 등을 만족시킨다.^[2]

누차 적분과의 관계[편집]

함수를 먼저 일부 변수에 대하여 적분한 뒤, 다시 남은 변수에 대하여 적분하는 것을 누차 적분(累次積分, 영어: repeated integral) 또는 반복 적분(反復積分)이라고 한다. 중적분은 일정 조건 아래 누차 적분을 통해 구할 수 있다.

함수 $fcolon Eto {mathbb R}$ ( ${displaystyle Esubseteq mathbb {R} ^{n}}$ 는 조르당 가측 집합)가 다음 두 조건을 만족시킨다고 하자.

$f$ 는 $E$ 에서 리만 적분 가능 함수이다.
임의의 ${displaystyle (x_{1},dots ,x_{n})in E}$ 에 대하여, 리만 적분 ${displaystyle overbrace {iint cdots int } _{{(x_{m+1},dots ,x_{n})colon (x_{1},dots ,x_{n})in E}}^{n-m}f(x_{1},dots ,x_{n})dx_{m+1}cdots dx_{n}}$ 이 존재한다.

그렇다면, 다음이 성립한다.^[2]

{displaystyle overbrace {iint cdots int } _{E}^{n}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=overbrace {iint cdots int } _{{(x_{1},dots ,x_{m})colon (x_{1},dots ,x_{n})in E}}^{m}dx_{1}cdots dx_{m}overbrace {iint cdots int } _{{(x_{m+1},dots ,x_{n})colon (x_{1},dots ,x_{n})in E}}^{n-m}f(x_{1},dots ,x_{n})dx_{m+1}cdots dx_{n}}

적분 구역 a ≤ x ≤ b, α(x) ≤ y ≤ β(x) 위의 적분은 x를 고정한 채 y에 대하여 적분한 뒤, 이를 다시 x에 대하여 적분한 것과 같다.

일부 특수한 정의역의 경우는 다음과 같다. (여기서 ${displaystyle phi leq psi }$ , ${displaystyle sigma leq tau }$ )

${displaystyle iint _{[a,b]times [c,d]}f(x,y)dxdy=int _{a}^{b}dxint _{c}^{d}f(x,y)dy}$
${displaystyle iint _{{(x,y)colon aleq xleq b,phi (x)leq yleq psi (x)}}f(x,y)dxdy=int _{a}^{b}dxint _{phi (x)}^{psi (x)}f(x,y)dy}$
${displaystyle iint _{{(x,y)colon aleq yleq b,phi (y)leq xleq psi (y)}}f(x,y)dxdy=int _{a}^{b}dyint _{phi (y)}^{psi (y)}f(x,y)dx}$
${displaystyle iiint _{{(x,y,z)colon (x,y)in Omega ,phi (x,y)leq zleq psi (x,y)}}f(x,y,z)dxdydz=iint _{Omega }dxdyint _{phi (x,y)}^{psi (x,y)}f(x,y,z)dz}$
${displaystyle iiint _{{(x,y,z)colon (x,z)in Omega ,phi (x,z)leq yleq psi (x,z)}}f(x,y,z)dxdydz=iint _{Omega }dxdzint _{phi (x,z)}^{psi (x,z)}f(x,y,z)dy}$
${displaystyle iiint _{{(x,y,z)colon (y,z)in Omega ,phi (y,z)leq xleq psi (y,z)}}f(x,y,z)dxdydz=iint _{Omega }dydzint _{phi (y,z)}^{psi (y,z)}f(x,y,z)dx}$
${displaystyle iiint _{{(x,y,z)colon aleq xleq b,(y,z)in Omega _{x}}}f(x,y,z)dxdydz=int _{a}^{b}dxiint _{Omega _{x}}f(x,y,z)dydz}$
${displaystyle iiint _{{(x,y,z)colon aleq yleq b,(x,z)in Omega _{y}}}f(x,y,z)dxdydz=int _{a}^{b}dyiint _{Omega _{y}}f(x,y,z)dxdz}$
${displaystyle iiint _{{(x,y,z)colon aleq zleq b,(x,y)in Omega _{z}}}f(x,y,z)dxdydz=int _{a}^{b}dziint _{Omega _{z}}f(x,y,z)dxdy}$
${displaystyle iiint _{{(x,y,z)colon aleq xleq b,phi (x)leq yleq psi (x),sigma (x,y)leq zleq tau (x,y)}}f(x,y,z)dxdydz=int _{a}^{b}dxint _{phi (x)}^{psi (x)}dyint _{sigma (x,y)}^{tau (x,y)}f(x,y,z)dz}$

그러나, 둘째 전제가 없다면 결론이 성립하지 않을 수 있다. 예를 들어, 다음과 같은 함수를 정의하자.

{displaystyle f(x,y)={begin{cases}x&(x,y)in {1,1/2,1/3,dots }times mathbb {Q} 0&(x,y)not in {1,1/2,1/3,dots }times mathbb {Q} end{cases}}}

그렇다면,

{displaystyle iint _{[0,1]times [0,1]}f(x,y)dxdy=0}

{displaystyle int _{0}^{1}dyint _{0}^{1}f(x,y)dx=0}

이지만, ${displaystyle f(1/n,y)=1_{mathbb {Q} }(y)/n}$ ( $n=1,2,dots$ )가 리만 적분 가능 함수가 아니므로

{displaystyle int _{0}^{1}dxint _{0}^{1}f(x,y)dy}

는 존재하지 않는다.

치환 적분[편집]

극좌표계

원통 좌표계

구면 좌표계

변수 변환 문서를 참고하십시오.

함수 ${displaystyle gcolon Eto mathbb {R} ^{n}}$ ( ${displaystyle Esubseteq mathbb {R} ^{n}}$ 는 조르당 가측 닫힌집합) 및 ${displaystyle fcolon g(E)to mathbb {R} }$ 가 다음 조건들을 만족시킨다고 하자.

$g$ 는 단사 $mathcal C^1$ 함수이다.
임의의 ${displaystyle tin D}$ 에 대하여, ${displaystyle det J_{g}(t)neq 0}$
$f$ 는 ${displaystyle g(E)}$ 에서 리만 적분 가능 함수이다.

그렇다면, 다음이 성립한다.

{displaystyle int _{g(E)}f(x)dx=int _{E}f(g(t))left|det J_{g}(t)right|dt}

여기서 ${displaystyle det J_{g}}$ 는 $g$ 의 야코비 행렬식인데, 어떤 점에서의 야코비 행렬식의 값은 대략 변환이 그 점 주위의 초부피를 확대시키는 배수를 나타낸다.

예를 들어, 극좌표 변환

{displaystyle x=rcos theta }

{displaystyle y=rsin theta }

{displaystyle det {frac {partial (x,y)}{partial (r,theta )}}={begin{vmatrix}cos theta &-rsin theta sin theta &rcos theta end{vmatrix}}=r}

에 의한 치환 적분 공식은 다음과 같다.

{displaystyle iint _{D}f(x,y)dxdy=iint _{g^{-1}(D)}f(rcos theta ,rsin theta )rdrdtheta }

또한, 원통 좌표 변환

{displaystyle x=rcos theta }

{displaystyle y=rsin theta }

{displaystyle z=z}

{displaystyle det {frac {partial (x,y,z)}{partial (r,theta ,z)}}=r}

에 의한 치환 적분 공식은 다음과 같다.

{displaystyle iiint _{D}f(x,y,z)dxdydz=iiint _{g^{-1}(D)}f(rcos theta ,rsin theta ,z)rdrdtheta }

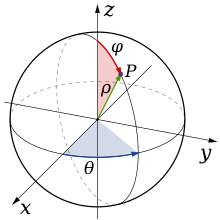
또한, 구면 좌표 변환

{displaystyle x=rcos theta sin varphi }

{displaystyle y=rsin theta sin varphi }

{displaystyle z=rcos varphi }

{displaystyle det {frac {partial (x,y,z)}{partial (r,theta ,varphi )}}=-r^{2}sin varphi }

에 의한 치환 적분 공식은 다음과 같다.

{displaystyle iiint _{D}f(x,y,z)dxdydz=iiint _{g^{-1}(D)}f(rcos theta sin varphi ,rsin theta sin varphi ,rcos varphi )r^{2}sin varphi drdtheta dvarphi }

기하학적 성질[편집]

음이 아닌 값의 함수 $fcolon Eto {mathbb R}$ ( ${displaystyle Esubseteq mathbb {R} ^{n}}$ 는 조르당 가측 집합)의 리만 중적분은 밑면이 정의역, 윗면이 함수의 그래프인 도형의 조르당 측도와 같다.

{displaystyle iint cdots int _{E}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}=operatorname {m} ({(x_{1},dots ,x_{n+1})colon (x_{1},dots ,x_{n})in E,;0leq x_{n+1}leq f(x_{1},dots ,x_{n})})}

특히, 상수 함수 1의 리만 중적분은 정의역의 조르당 측도와 같다.

{displaystyle iint cdots int _{E}dx_{1}cdots dx_{n}=operatorname {m} (E)}

이상 중적분의 성질[편집]

이상 중적분 역시 중적분과 비슷한 성질들을 만족시킨다.

예를 들어, 함수 ${displaystyle fcolon [a,infty )times [b,infty )to mathbb {R} }$ 가 다음 조건을 만족시킨다고 하자.

임의의 조르당 가측 닫힌집합 ${displaystyle Fsubseteq [a,infty )times [b,infty )}$ 에 대하여, $f$ 는 $F$ 에서 리만 적분 가능 함수이다.

그렇다면, 다음이 성립한다.^[3]^{:175, 定理15.5.4}

만약 ${displaystyle int _{a}^{infty }dxint _{b}^{infty }|f(x,y)|dy<infty }$ 라면, ${displaystyle iint _{[a,infty )times [b,infty )}f(x,y)dxdy=int _{a}^{infty }dxint _{b}^{infty }|f(x,y)|dy}$
만약 ${displaystyle int _{a}^{infty }dxint _{b}^{infty }|f(x,y)|dy=infty }$ 라면, ${displaystyle iint _{[a,infty )times [b,infty )}f(x,y)dxdy}$ 는 발산한다.

또한, 무계 닫힌집합 ${displaystyle Esubseteq mathbb {R} ^{n}}$ 및 단사 $mathcal C^1$ 함수 ${displaystyle gcolon Eto mathbb {R} ^{n}}$ 및 함수 ${displaystyle fcolon g(E)to mathbb {R} }$ 에 대하여, 만약 두 이상 적분

{displaystyle iint cdots int _{g(E)}f(x)dx=iint cdots int _{E}f(g(t))left|det J_{g}(t)right|dt}

가운데 하나가 존재한다면, 남은 하나도 존재하며, 이 둘은 서로 같다.^[3]^{:175, 정리 15.5.5}

이상 리만 중적분

{displaystyle iint cdots int _{E}f(x_{1},dots ,x_{n})dx_{1}cdots dx_{n}}

이 수렴할 필요충분조건은

{displaystyle iint cdots int _{E}|f(x_{1},dots ,x_{n})|dx_{1}cdots dx_{n}<infty }

이다. 즉, 일변수 함수의 경우와 달리, 이상 리만 중적분이 수렴할 필요충분조건은 절대 수렴이다.

예[편집]

직육면체의 부피[편집]

직육면체 ${displaystyle [0,1]times [0,2]times [0,3]}$ 의 부피를 중적분을 통해 다음과 같이 구할 수 있다.

{displaystyle {begin{aligned}iiint _{[0,1]times [0,2]times [0,3]}dxdydz&=int _{0}^{1}dxint _{0}^{2}dyint _{0}^{3}dz&=int _{0}^{1}dxint _{0}^{2}3dy&=int _{0}^{1}6dx&=6end{aligned}}}

삼각뿔의 부피[편집]

삼각뿔 ${displaystyle {(x,y,z)colon 0leq x,y,zleq x+y+zleq 1}}$ 의 부피를 중적분을 통해 다음과 같이 구할 수 있다.

{displaystyle {begin{aligned}iiint _{{(x,y,z)colon 0leq x,y,zleq x+y+zleq 1}}dxdydz&=int _{0}^{1}dxint _{0}^{1-x}dyint _{0}^{1-x-y}dz&=int _{0}^{1}dxint _{0}^{1-x}(1-x-y)dy&=int _{0}^{1}{frac {(1-x)^{2}}{2}}dx&={frac {1}{6}}end{aligned}}}

이차 곡면으로 둘러싸인 도형의 부피[편집]

타원 포물면 z = x² + y²와 원기둥 x² + y² = a²에 의해 둘러싸인 도형

구 x² + y² + z² = a²와 원뿔 z² = (x² + y²)tana에 의해 둘러싸인 도형

타원 포물면과 원기둥으로 둘러싸인 도형 ${displaystyle {(x,y,z)colon 0leq zleq x^{2}+y^{2}leq a^{2}}}$ 의 부피를 중적분을 통해 다음과 같이 구할 수 있다.

{displaystyle {begin{aligned}iiint _{{(x,y,z)colon 0leq zleq x^{2}+y^{2}leq a^{2}}}dxdydz&=int _{0}^{a}rdrint _{0}^{2pi }dtheta int _{0}^{r}dz&=int _{0}^{a}r^{2}drint _{0}^{2pi }dtheta &=int _{0}^{a}2pi r^{2}dr&={frac {2}{3}}pi a^{3}end{aligned}}}

구와 원뿔로 둘러싸인 도형 ${displaystyle textstyle left{(x,y,z)colon {sqrt {x^{2}+y^{2}}}cot alpha leq zleq {sqrt {a^{2}-x^{2}-y^{2}}}right}}$ 의 부피를 중적분을 통해 다음과 같이 구할 수 있다.